Increased Productivity Example
#8
Body Plasma Chemistry [1]
Problem Statement: Determine the concentration of a Therapeutic treatment drug - and for that matter any drug - that is in the body over a period of time by finding:
1. The rate constant (Ka) that determines the diffusion of therapeutic treatment drug from the stomach into the blood-stream (plasma);
2. The rate at which the drug enters and leaves the tissues, K12 and K21;
3. The loss of therapeutic treatment drug into the urine, K1;
4. The break-down of therapeutic treatment drug into conjugated form and DEGT, K2 + K3;
5. The volume of blood, V.
?? 6. The binding or non-binding of the drug with free proteins in the plasma K??
The body tissues utilize the drug and therefore an amount is removed by the body's filtering system, i.e. the Kidneys and urine. As with most compounds, some binding with proteins can occur, as well as conjugation and degradation of the drug. This will also provide information as to how often the treatment drug needs to be administered to keep the concentration high enough to allow for the required treatment to occur.
Given: Observed values (concentrations) for the plasma levels of the therapeutic treatment drug; observed accumulated values (amounts) of the therapeutic treatment drug, conjugated therapeutic treatment drug and DEGT (degraded therapeutic treatment drug); and the dose of therapeutic treatment drug.
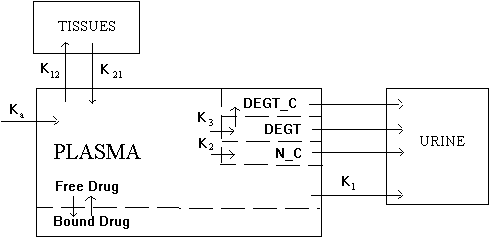
NPt = Total therapeutic treatment drug in plasma
NPf = Free therapeutic treatment drug in plasma
NT = therapeutic treatment drug in tissues
Nu = therapeutic treatment drug excreted
N_Cu = Conjugated therapeutic treatment drug excreted
DEGTu = Total (free and conjugated) DEGT excreted
D = Dose of therapeutic treatment drug
V = Volume of distribution
Pn = Protein binding constants
Constraints:
[NPf] = f( [NPt], P1, P2, P3, P4)
d[NPt]/dt = Ka *D/V * e ^ (-Ka*t) - K12 [NPf] + K21 [NT] - (K1 + K2 +
K3) [NPf]
d[NT]/dt = K12 [NPf] - K21 [NT]
d[Nu]/dt = K1 V [NPf]
d[N_Cu]/dt = K2 V [NPf]
d[DEGTu]/dt = K3 V [NPf]
where "[ X ]" implies Concentration of X
and Ky represent Rate constants, y = a, 12, 21, 1, 2 & 3
Bound Therapeutic Treatment Drug is that portion of Therapeutic treatment drug in the plasma that is bound to protein and thus unable to participate in other reactions. In analyzing blood samples, no distinction can be made between free [NPf] and protein-bound therapeutic treatment drug and thus the observed values are total therapeutic treatment drug [NPt]. The function that relates NPf to NPt is shown in the 1st equation. It involves finding a root of a 3rd order polynomial, the coefficients of which are functions of NPt and the four protein binding constants.
The four reactions involving N_C, DEGT and DEGT_C that are shown without a rate constant are non-limiting reactions and assumed to be instantaneous. No distinction is made between free DEGT and conjugated DEGT (DEGT_C), they are simply totaled as DEGT in the model.
Increased Productivity Example #8 Source Code:
Problem .Therapeutic.Drug.Concentration
local b
execute .Initialize
b = .Data( .05, 1, .005, .1, .5, .5, 50)
Find k, v in .DrugModel under .Optcont with bounds b to minimize error
End
Model .DrugModel
local i, j
plasma = 0 tissue = 0 excret = 0 error = 0
bsamp = 1 usamp = 1 time = 0 dt = dtstart
Initiate Gemini under .StepSize for .Kinetics
equations dplasma / plasma, dtissue / tissue, dexcret / excret
of time step dt to tnext
execute .Tprint
for i = 1 to nb + nu do
if samptype(i) is blood then
tnext = bloodtime( bsamp)
integrate .Kinetics
error.b( bsamp) = plasma / obs.plasma( bsamp) - 1
es = error.b( bsamp)**2 w = dplasma**2 + 1
we = es / w error = error + es
if bloodtime( bsamp) ne urinetime( usamp) execute .Bprint
bsamp = bsamp + 1
else
tnext = urinetime( usamp)
integrate .Kinetics
for j = 1 to 3 do
error.u( usamp, j) = excret(j) / obs.excret( usamp, j) - 1
es = ( error.u( usamp, j)**2 ) / weight
w = dexcret(j)**2 + 1 we = es / w error = error + es
repeat
if urinetime( usamp) ne bloodtime( bsamp - 1)
then execute .Uprint
else execute .Buprint
close
usamp = usamp + 1
close
repeat
oldk = k oldv = v
execute .Eprint olderror = error
end [.DrugModel]
Model .Kinetics
execute .ProBind
dtissue = k(2) * free - k(3) * tissue
dplasma = k(1) * dose / v * .Exp(-k(1)*time) - (k(4)+k(5)+k(6))* free - dtissue
dexcret(1) = k(4) * free * v dexcret(2) = k(5) * free * v
dexcret(3) = k(6) * free * v
end
Model .ProBind
a = ap - plasma b = bp + bp2 * plasma c = cp * plasma
free = plasma / 10
for ii = 1 to 20 do
xu = ((free + a) * free + b) * free + c
xl = (3 * free + 2 * a) * free + b
xu = xu / xl free = free - xu
if .Abs( xu) lt .005 * free exit
repeat
free = free + xu / 2
end
Controller .Optcont for Hera
detail = 1 detout = 0 maxit = 7 adjust = 2 improve = 5.e-4
End
Controller .StepSize for Gemini
maxerr = .0001
end
Procedure .Tprint
eject 'Calculated values for this simulation.' Page
vector print k, v
dk = .Sub( oldk, k) rdk = .Div( dk, k) rdk = .Mul( rdk, 100)
dv = oldv - v rdv = dv / v * 100
skip 4 lines
display (for i = 1 to 6, k(i)), v, (for i = 1 to 6, dk(i)), dv,
(for i = 1 to 6, rdk(i)), rdv in
' k(1) k(2) k(3) k(4) k(5) k(6) v'
' Value: **.*** ***.** **.**** **.*** ***.*** **.*** ****',
' Change: **.*** ***.** **.**** **.*** ***.*** **.*** ****',
' PrCnt Chg: **.** **.** **.** **.** **.** **.** **.**'
skip 4 lines
text print 'Time ---Therapeutic treatment drug, Micrograms/Milliliter[
]------- cum. amounts excreted, Milligrams Ttd equiv----'
text print ' Hrs ------Plasma------ -Tissue- --Free-- -----Therapeutic [
]treatment drug----- ----Conjugated---- -----Total DEGT----'
end [.Tprint]
Procedure .Bprint
local i
display time, plasma*1000, error.b( bsamp)*100, tissue*1000, free*1000
in ' ** ****.*** (****.**) ****.*** **.***** [
] --- --- --- --- --- ---'
end
Procedure .Uprint
local i, erru Allot erru(3)
for i = 1 to 3 erru(i) = error.u( usamp, i) *100
display time,excret(1), erru(1), excret(2), erru(2), excret(3), erru(3)
in ' ** --- --- --- --- [
] ****.***.(**** **) ****.***.(**** **) ****.***.(**** **)'
end
Procedure .BUprint
local i, erru Allot erru(3)
for i = 1 to 3 erru(i) = error.u( usamp, i) *100
display time, plasma*1000, error.b( bsamp-1)*100, tissue*1000, free*1000
excret(1), erru(1), excret(2), erru(2), excret(3), erru(3)
in ' ** ****.*** (****.**) ****.*** **.***** [
] ****.***.(**** **) ****.***.(**** **) ****.***.(**** **)'
end
Procedure .Eprint
de = error -olderror rde = de * 100 / error
skip 4 lines
display error, de, rde,
in 'Error: ***.******; Change: ***.*****; % Change: ***.*****'
end
Procedure .Initialize
blood = 1 urine = 2 weight = 1
read data
allot bloodtime(nb), obs.plasma(nb), error(nb)
allot urinetime(nu), obs.excret(nu,3), error.u(nu,3)
allot excret(3), dexcret(3), samptype(nb+nu)
allot p(4), k(6), oldk(6), dk(6), rdk(6)
read data
oldk = k oldv = v
ap = p(1) + p(2) + p(3) + p(4)
bp = p(1) * p(4) + p(2) * p(3) + p(2) * p(4)
bp2 = -(p(2) + p(4)) cp = - p(2) * p(4)
display dose, dtstart, nb, nu, blood, urine, ap, bp, bp2, cp in
'**** *.*** * * * * *.***E*** *.***E*** **.***E*** **.***E***'
vector print p, bloodtime, obs.plasma, urinetime, obs.excret, samptype
End
This Body Plasma problem is another increased productivity example do to using Calculus (level) programming. Try it, you'll love it!
[1] Wolski, D. and Petersen, D.M.
HTML code for linking to this page:
<a
href="https://goal-driven.net/example/body-plasma.html"><img
style="float:left; width:100px"
src="http://goal-driven.net/image/fc-compiler-icon.png"/>
<strong>Body Plasma Chemistry</strong> </a>, determine the concentration of a Therapeutic treatment drug.
|
|