Pilot Ejection from aircraft demo
Pilot Ejection Equations of motion
_________
Using a calculus level language, e.g. FC-Compiler, we'll show how to solve linear, nonlinear, implicit, algebraic, laplace transforms, differential equations, or systems of such equations in a minimum of time while tweaking parameter(s) to meet user's requirements. Most math models may be solved in a few days, once your equations are ready for compiling.
Solution accuracy improves due to the behind the scene use of Automatic Differentiation (AD). For a mental picture of what's going on, think of AD as taking symbolic derivatives of the equations involved in your model and evaluating these derivatives at given points. Derivative accuracy is thus as accurate as your computer allows.
Key statements for Calculus-level Programming:
The 'Find ...' statement is key to Calculus-level programming.
Find a, b, c, ...; in Seat; ...
This is a general form where 'a, b, c, ...' represent parameters to vary in routine/model 'Seat' until objective/goal is achieved; i.e. gx=0 & gy=0 (see code below).
Enjoy learning Calculus-level Programming!
Pilot Eject Equations Source Code:
global all
problem eject ! pilot ejection profile
C ------------------------------------------------------------------------
C --- Calculus Programming example: ODE Boundary value problem
C ------------------------------------------------------------------------
dimension alt(6),vel(6)
character fcsint*2,plane*7
data alt/0,10000,20000,30000,40000,50000/
smass=7 : g=32.2 : cd=1 : ve=40 : thetad=15 : time=1.0
s=10 : y1=4 : va=100
do 10 i=1,6
h=alt(i) : it=0 : plane='plane'//fcsint(i)
@axes(plane,'Pilot Ejection')
if(h.le.35332) then
rho=0.002378*(1-.689e-5*h)**4.256
else
rho=0.00315/exp(1.452+(h-35332)/20950)
end if
Find va,time; in seat(plane); by AJAX(acon); to match gx,gy
@display(plane)
vel(i)=va
10 continue
@safe('profile')
end
controller acon(AJAX)
damp=0
end
model seat(plane)
character*2 fcsint,ni,plane*7
vx=sqrt(va**2)-ve*sind(thetad) : vy=ve*cosd(thetad)
v=sqrt(vx*vx+vy*vy) : theta=atan(vy/vx)
x=0 : y=y1 : t=0 : dt=abs(time)/20 : dp=4*dt : tp=t+dp
it=it+1 : ni=fcsint(it)
if(it.gt.9) then
@point(plane,'i'//ni,x,y)
else
@curve(plane,'i'//ni,x,y)
end if
initiate isis; for motion; equations
& thedot/theta, vdot/v, xdot/x, ydot/y; of t; step dt; to tp
do while (t.lt.time)
integrate motion; by isis
@curve(plane,'i'//ni,x,y)
tp=tp+dp
end do
gx=-x-30 ! boundary condition on x at t=time
gy=y-20 ! boundary condition on y at t=time
terminate motion
end
model motion ! differential equations
d=0.5*rho*cd*s*v*v
thedot=-g*cos(theta)/v
vdot=-d/smass-g*sin(theta)
xdot=v*cos(theta)-abs(va)
ydot=v*sin(theta)
end
The above code finds a math solution to this problem.
The next code displays some graphs to help user 'picture' what is going on. These graphs are not required to solve this problem.
procedure axes(name,title)
character*(*) name,title
dimension p1(2,6),p2(2,11),tg(2,9)
data p1/8.7,0,8.9,.5,7.75,1.5,5,2.2,2.2,3.8,1.8,2.8/
data p2/5,2.2,1.8,2.8,.25,3.1,-0.1,4.0,-21,3.75,-25,3.9,
& -26.3,4.75,-29.2,11,-30,12,-32.2,12,-30.3,0/
data tg/-30.6,19.4,-30,19.15,-29.4,19.4,-30.6,20.6,-30,20.85,
& -29.4,20.6,-30.6,19.4,-30.85,20,-30.6,20.6/
@graph(name,'2dgraph')
@chrsize(0.05)
@frame(0,.5,5,4)
@window(name,50,500,30,400,-30,0,0,30,0,0,0,1,1.5)
@xaxis(name,-30,0,10,0,1,1)
@yaxis(name,0,30,10,0,1,1)
@setup(name,'i1',0,11,-2,0) ! 1st iteration (blue)
@setup(name,'i2',0,2,-2,0) ! 2nd iteration (green)
@setup(name,'i3',0,3,-2,0) ! 3rd iteration (cyan)
@setup(name,'i4',0,4,-2,0) ! 4th iteration (red)
@setup(name,'i5',0,5,-2,0) ! 5th iteration (magenta)
@setup(name,'i6',0,6,-2,0) ! 6th iteration (orange)
@setup(name,'i7',0,7,-2,0) ! 7th iteration (white)
@setup(name,'i8',0,9,-2,0) ! 8th iteration (light blue)
@setup(name,'i9',0,10,-2,0) ! 9th iteration (light green)
@setup(name,'p1',0,7,-2,0) ! plane outline 1 (light blue)
@setup(name,'p2',0,7,-2,0) ! plane outline 2 (light blue)
@setup(name,'tg',0,12,-2,0) ! target (light red)
@label(name,20,title,7,50,420,0)
@label(name,8,'Altitude',7,200,400,0)
@number(name,300,400,h,8)
do 10 j=1,6
@curve(name,'p1',p1(1,j),p1(2,j))
10 continue
do 20 j=1,11
@curve(name,'p2',p2(1,j),p2(2,j))
20 continue
do 30 j=1,9
@curve(name,'tg',tg(1,j),tg(2,j))
30 continue
return
C
entry display(name)
@label(name,5,'Speed',7,200,380,0)
@number(name,300,380,va,8)
@show(name)
end
procedure safe(gname)
character*(*) gname
@graph(gname,'2dgraph')
@window(gname,100,500,50,400,200,800,0,50000,200,0,0,1,1.5)
@xaxis(gname,200,800,200,0,1,1)
@yaxis(gname,0,50000,10000,0,1,1)
@xclabel(gname,5,'Speed',7)
@yelabel(gname,8,'Altitude',7)
@setup(gname,'pp',0,0,ichar('*'),14) ! profile points (yellow *'s)
@setup(gname,'cr',0,10,-2,0) ! profile curve (light green)
@label(gname,21,'Safe Ejection Profile',7,150,420,0)
do 10 j=1,6
@point(gname,'pp',vel(j),alt(j))
@curve(gname,'cr',vel(j),alt(j))
10 continue
@show(gname)
end
Pilot Ejection Equations Output:
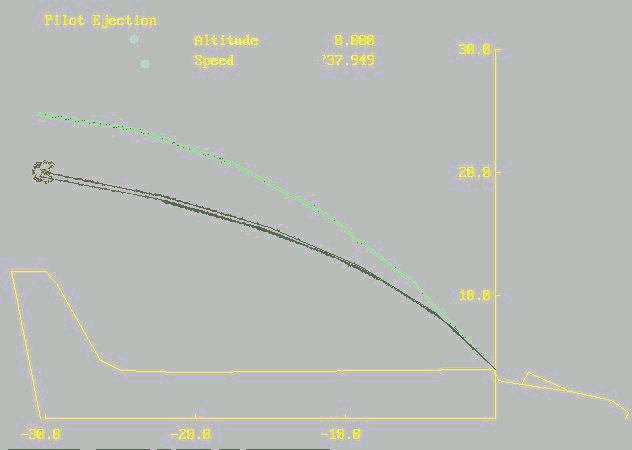
Output shows several plot files (like this one to the right) and a summary plot titled 'Safe Ejection Profile'. Plots require a lot of code relative to solving a math problem! Fortunately, basic plot code is easily copied between apps with minor changes to code.
(DO 10 i=1,6 ... 1st loop output from 'find' stmt.)
--- AJAX SUMMARY, INVOKED AT EJECT[25] FOR MODEL SEAT ----
CONVERGENCE CONDITION AFTER 5 ITERATIONS
UNKNOWNS CONVERGED
CONSTRAINTS SATISFIED
ALL SPECIFIED CRITERIA SATISFIED
LOOP NUMBER ......... [INITIAL] 1 2
UNKNOWNS
VA 1.000000E+02 2.536099E+02 2.502373E+02
TIME 1.000000E+00 4.889347E-01 6.185860E-01
CONSTRAINTS
GX 5.923573E-01 -7.837109E+00 3.713794E-01
GY 4.787695E+00 -2.346940E+00 -3.065783E-01
LOOP NUMBER ......... [INITIAL] 3 4
UNKNOWNS
VA 1.000000E+02 2.377807E+02 2.379490E+02
TIME 1.000000E+00 6.344608E-01 6.345711E-01
CONSTRAINTS
GX 5.923573E-01 -2.705302E-02 1.297491E-05
GY 4.787695E+00 -4.164254E-05 -4.704651E-07
LOOP NUMBER ......... [INITIAL] 5
UNKNOWNS
VA 1.000000E+02 2.379489E+02
TIME 1.000000E+00 6.345710E-01
CONSTRAINTS
GX 5.923573E-01 2.923883E-12
GY 4.787695E+00 -1.421085E-14
---END OF LOOP SUMMARY
--- AJAX SUMMARY, INVOKED AT EJECT[25] FOR MODEL SEAT ----
CONVERGENCE CONDITION AFTER 3 ITERATIONS
UNKNOWNS CONVERGED
CONSTRAINTS SATISFIED
ALL SPECIFIED CRITERIA SATISFIED
LOOP NUMBER ......... [INITIAL] 1 2
UNKNOWNS
VA 2.379489E+02 2.815858E+02 2.806970E+02
TIME 6.345710E-01 6.203815E-01 6.192025E-01
CONSTRAINTS
GX -3.184507E+00 1.722351E-01 4.900175E-04
GY 4.815811E-01 1.101312E-02 -3.919713E-05
LOOP NUMBER ......... [INITIAL] 3
UNKNOWNS
VA 2.379489E+02 2.806918E+02
TIME 6.345710E-01 6.192031E-01
CONSTRAINTS
GX -3.184507E+00 3.608125E-09
GY 4.815811E-01 1.031175E-10
---END OF LOOP SUMMARY
ooo
|
|

